Four Square Theorem - Quaternions, PDF, Prime Number
Por um escritor misterioso
Last updated 10 novembro 2024


Table 1 from Extended Lagrange's four-square theorem

Table 3 from Extended Lagrange's four-square theorem

Gaussian primes, Eisenstein primes and Hurwitz Primes

Exploring Number Theory the Pythagorean Way: Right Triangles, Sums of Squares, and Arithmetic by Educohack Press - Ebook
What are the elements of the cosets of the subgroup {1, −1} of the group of quaternions {1,-1,I,-i,j,-j, k,-k}? - Quora

PDF) A Simple Proof of Jacobi's Four-Square Theorem

Topics in Algebraic Number Theory Part 12 - ALGEBRAIC NUMBER THEORY LECTURE 12 NOTES 1. Section 5. - Studocu

References - Why Is There Philosophy of Mathematics At All?

Discrete quantum computation and Lagrange's four-square theorem

PDF) The history of the 2-, 4- and 8-square identities
Are there any primes that can't be expressed with quaternion factors? If so, what are some examples? - Quora

A Pythagorean Introduction to Number Theory

Exploiting Quaternions to Support Expressive Interactive Character

PDF) New parametrization of A2 + B2 + C2 = 3D2 and langrange's four-square theorem

MathType - Lagrange's four-square theorem states that every natural number can be represented as the sum of four integer squares. Proved by Joseph Louis #Lagrange in 1770, it can be regarded as
Recomendado para você
-
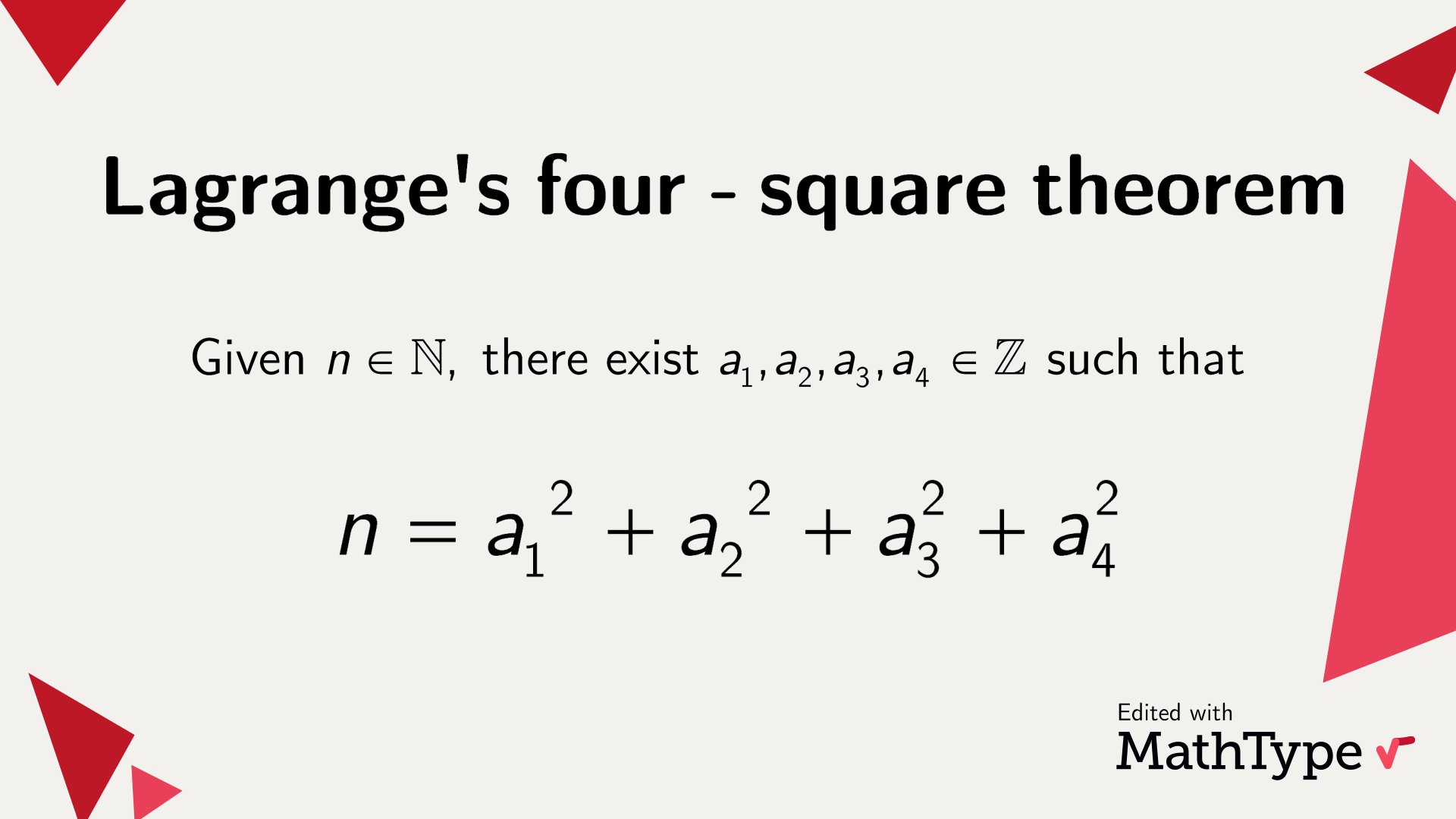 MathType on X: Lagrange's four-square theorem asserts that any positive whole number can be written as the sum of four squares of integers. Leave an example in the comments! #MathType #NumberTheory #math #10 novembro 2024
MathType on X: Lagrange's four-square theorem asserts that any positive whole number can be written as the sum of four squares of integers. Leave an example in the comments! #MathType #NumberTheory #math #10 novembro 2024 -
 Sums of four squares — AnhThu Nguyen10 novembro 2024
Sums of four squares — AnhThu Nguyen10 novembro 2024 -
Math & Physics - Lagrange's Four-square Theorem Follow instagram.com/ins.map.lb10 novembro 2024
-
 Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers10 novembro 2024
Lagrange's four-square theorem, polynomials, diophantine equations, prime numbers10 novembro 2024 -
 Square Number Definition & Meaning10 novembro 2024
Square Number Definition & Meaning10 novembro 2024 -
 Waring's Problem & Lagrange's Four-Square Theorem10 novembro 2024
Waring's Problem & Lagrange's Four-Square Theorem10 novembro 2024 -
 Discrete quantum computation and Lagrange's four-square theorem10 novembro 2024
Discrete quantum computation and Lagrange's four-square theorem10 novembro 2024 -
 Lagrange's Four-Square Theorem by Julian TSE10 novembro 2024
Lagrange's Four-Square Theorem by Julian TSE10 novembro 2024 -
 PPT - Combinatorial Geometry PowerPoint Presentation, free download - ID:488680810 novembro 2024
PPT - Combinatorial Geometry PowerPoint Presentation, free download - ID:488680810 novembro 2024 -
 Sum of squares, Part-2, Sum of four squares10 novembro 2024
Sum of squares, Part-2, Sum of four squares10 novembro 2024
você pode gostar
-
 FANTASY NIGHT PARTY (1) Template10 novembro 2024
FANTASY NIGHT PARTY (1) Template10 novembro 2024 -
 This Friday Is The 13th! Are You Ready? Book Review and Ratings by Kids - Kavi Dolasia10 novembro 2024
This Friday Is The 13th! Are You Ready? Book Review and Ratings by Kids - Kavi Dolasia10 novembro 2024 -
 The Batman 2022 Movie Wallpaper iPhone Phone 4K #6840e10 novembro 2024
The Batman 2022 Movie Wallpaper iPhone Phone 4K #6840e10 novembro 2024 -
 Play Golden Eyes by Kayla Reeves on Music10 novembro 2024
Play Golden Eyes by Kayla Reeves on Music10 novembro 2024 -
 TOP 5: Animes da temporada de primavera que você precisa ver10 novembro 2024
TOP 5: Animes da temporada de primavera que você precisa ver10 novembro 2024 -
 When you accidentally kill in among us, @minimemer3810 novembro 2024
When you accidentally kill in among us, @minimemer3810 novembro 2024 -
 welcome to my dark side — Ride The Storm - Act III of Hold Me Down10 novembro 2024
welcome to my dark side — Ride The Storm - Act III of Hold Me Down10 novembro 2024 -
 Steve Rubinstein – Antares Capital10 novembro 2024
Steve Rubinstein – Antares Capital10 novembro 2024 -
 História das mercadorias10 novembro 2024
História das mercadorias10 novembro 2024 -
 Stickman meme funny | Drawstring Bag10 novembro 2024
Stickman meme funny | Drawstring Bag10 novembro 2024
