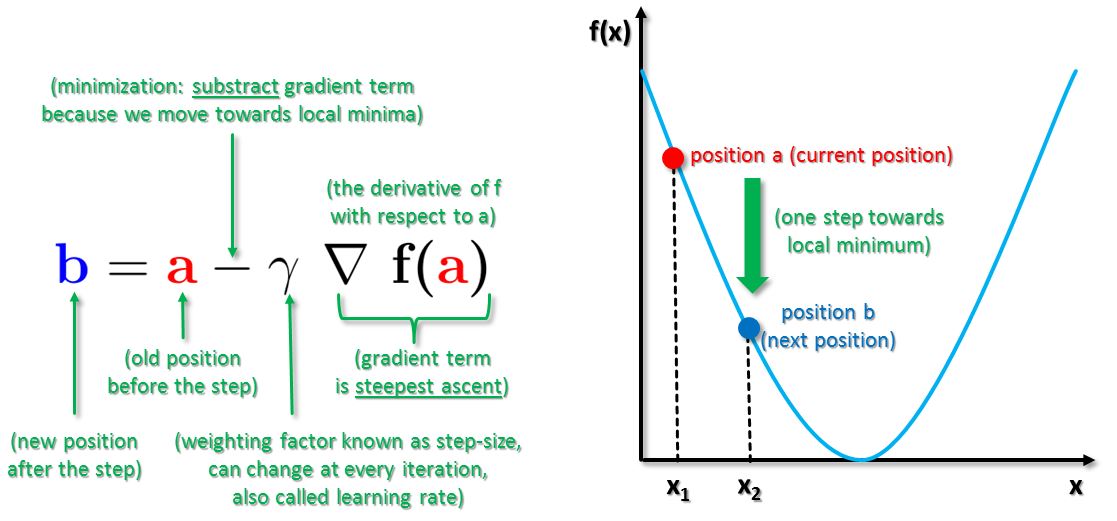
MathType - The #Gradient descent is an iterative optimization #algorithm for finding local minimums of multivariate functions. At each step, the algorithm moves in the inverse direction of the gradient, consequently reducing
Por um escritor misterioso
Last updated 23 abril 2025

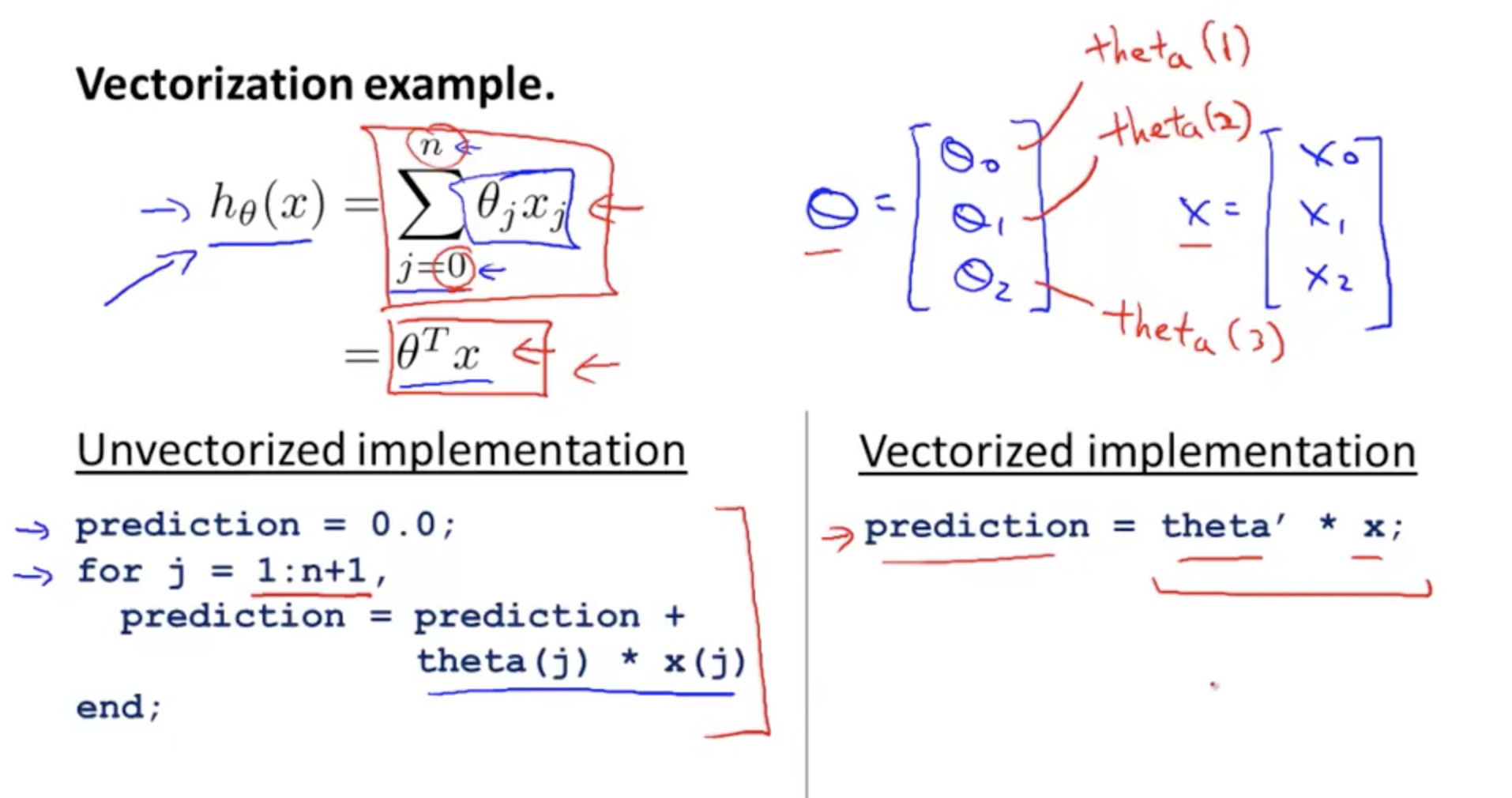
L2] Linear Regression (Multivariate). Cost Function. Hypothesis. Gradient

Gradient descent is a first-order iterative optimization algorithm for finding a local minimum of a differentiable function. To find a local minimum of a function using gradient descent, we take steps proportional
Solved] . 4. Gradient descent is a first—order iterative optimisation

Optimization Techniques used in Classical Machine Learning ft: Gradient Descent, by Manoj Hegde

Intuition (and maths!) behind multivariate gradient descent, by Misa Ogura

Solved 4. Gradient descent is a first-order iterative
Can gradient descent be used to find minima and maxima of functions? If not, then why not? - Quora

Task 1 Gradient descent algorithm: In this project
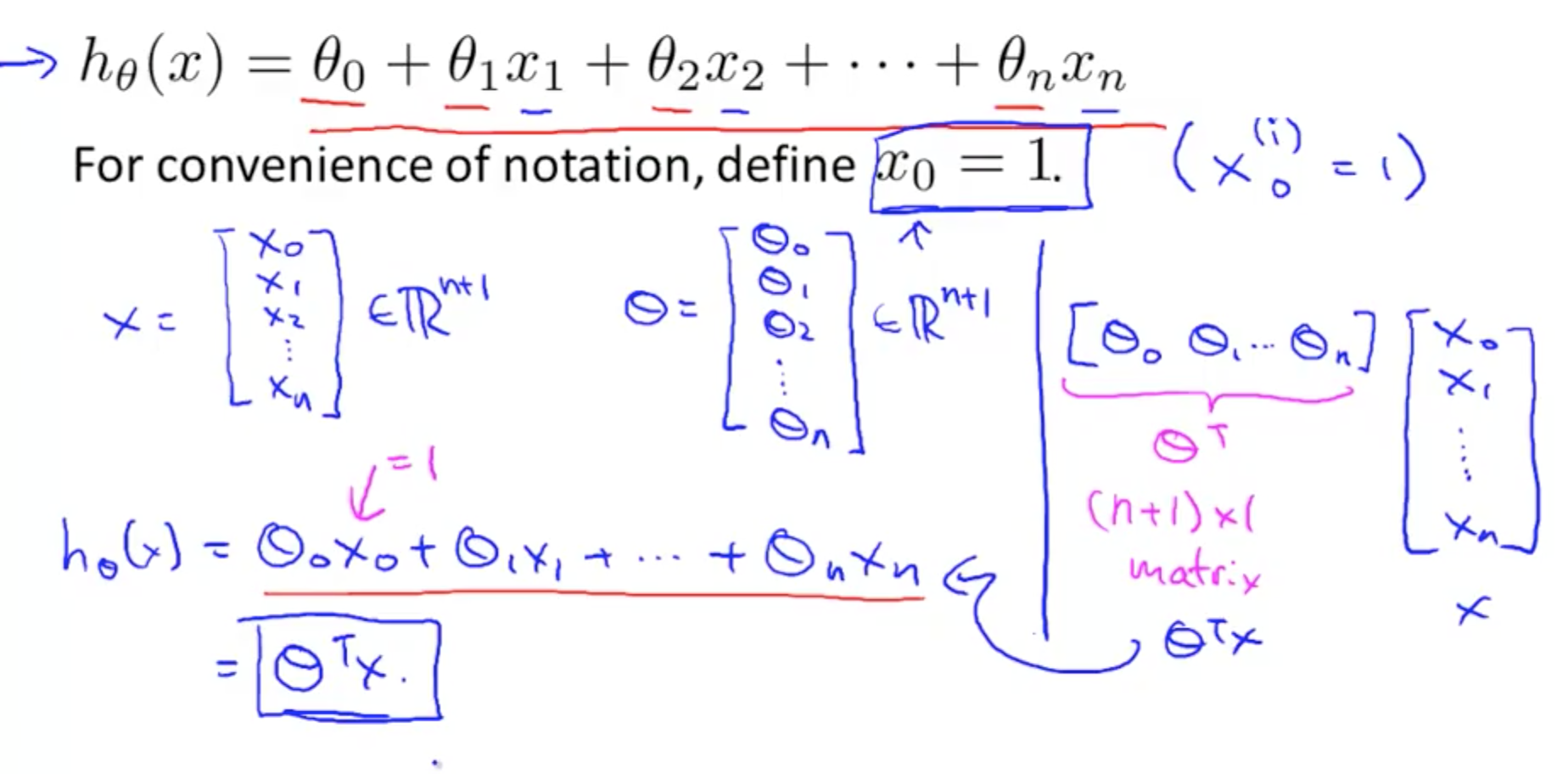
Linear Regression with Multiple Variables Machine Learning, Deep Learning, and Computer Vision

Linear Regression with Multiple Variables Machine Learning, Deep Learning, and Computer Vision
Gradient Descent Algorithm in Machine Learning - Analytics Vidhya
How to figure out which direction to go along the gradient in order to reach local minima in gradient descent algorithm - Quora
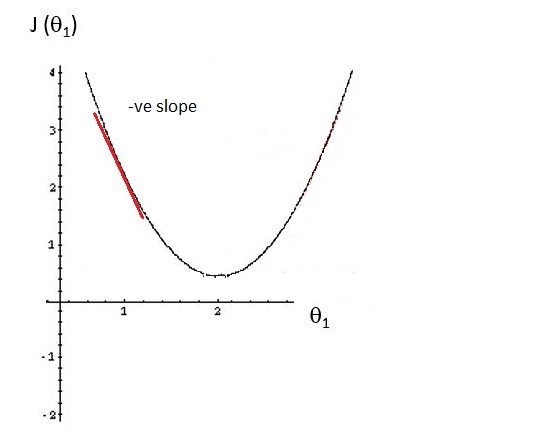
Gradient Descent Algorithm
Recomendado para você
-
 The steepest descent algorithm.23 abril 2025
The steepest descent algorithm.23 abril 2025 -
 Steepest Descent Method23 abril 2025
Steepest Descent Method23 abril 2025 -
 matrices - How is the preconditioned conjugate gradient algorithm related to the steepest descent method? - Mathematics Stack Exchange23 abril 2025
matrices - How is the preconditioned conjugate gradient algorithm related to the steepest descent method? - Mathematics Stack Exchange23 abril 2025 -
 Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings23 abril 2025
Lecture 15: Steepest Descent Method for Asymptotic Analysis (Chapter 15) - Lectures on Random Lozenge Tilings23 abril 2025 -
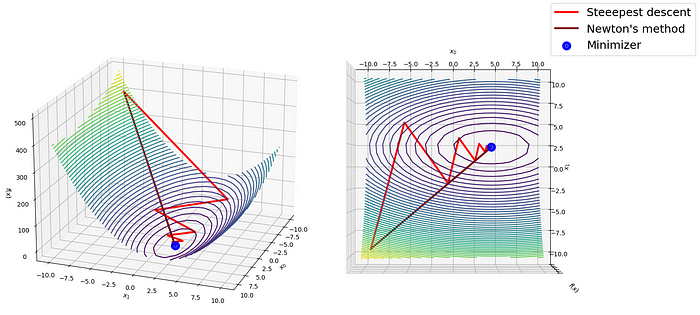 Steepest Descent and Newton's Method in Python, from Scratch: A… – Towards AI23 abril 2025
Steepest Descent and Newton's Method in Python, from Scratch: A… – Towards AI23 abril 2025 -
 PDF) Steepest Descent juan meza23 abril 2025
PDF) Steepest Descent juan meza23 abril 2025 -
 Gradient Descent Big Data Mining & Machine Learning23 abril 2025
Gradient Descent Big Data Mining & Machine Learning23 abril 2025 -
![PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning](https://d3i71xaburhd42.cloudfront.net/a0174a41c7d682aeb1d7e7fa1fbd2404e037a638/11-Figure8.1-1.png) PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning23 abril 2025
PDF] Steepest Descent and Conjugate Gradient Methods with Variable Preconditioning23 abril 2025 -
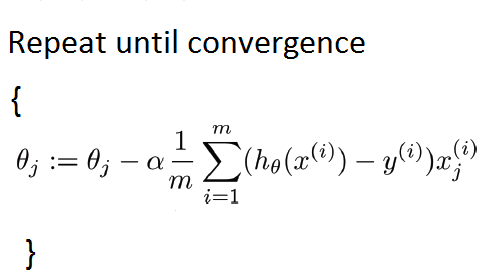 3 Types of Gradient Descent Algorithms for Small & Large Data Sets23 abril 2025
3 Types of Gradient Descent Algorithms for Small & Large Data Sets23 abril 2025 -
 Solving unconstrained optimization problems using steepest descent algorithm : r/optimization23 abril 2025
Solving unconstrained optimization problems using steepest descent algorithm : r/optimization23 abril 2025
você pode gostar
-
Como jogar com um mono Mordekaiser #wildriftbr23 abril 2025
-
 ACO Unopar o que é? Tudo que você precisa saber23 abril 2025
ACO Unopar o que é? Tudo que você precisa saber23 abril 2025 -
 Chainsaw Man': Anime ganha novo cartaz incrível e BRUTAL; Confira! - CinePOP23 abril 2025
Chainsaw Man': Anime ganha novo cartaz incrível e BRUTAL; Confira! - CinePOP23 abril 2025 -
 Hawaiian Spider Large Plant Green Spider Plant23 abril 2025
Hawaiian Spider Large Plant Green Spider Plant23 abril 2025 -
 🔥IDs de Funk (Pipoco) MUITO ID ‹ Roblox ›23 abril 2025
🔥IDs de Funk (Pipoco) MUITO ID ‹ Roblox ›23 abril 2025 -
 Pixilart - Canon DustDust sans by PizzaSlice0323 abril 2025
Pixilart - Canon DustDust sans by PizzaSlice0323 abril 2025 -
Batman Arkham City e Asylum 2 em 1 Original - Xbox 360 - Escorrega o Preço23 abril 2025
-
 Mamahaha no Tsurego ga Motokano datta - My Stepmom's Daughter Is23 abril 2025
Mamahaha no Tsurego ga Motokano datta - My Stepmom's Daughter Is23 abril 2025 -
 Nomes curtos masculinos - Tendências 202323 abril 2025
Nomes curtos masculinos - Tendências 202323 abril 2025 -
 GIFMaker.me, Toolur23 abril 2025
GIFMaker.me, Toolur23 abril 2025
